1868. Function

Calculate the function:

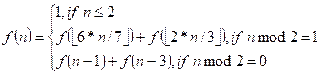
Input. One positive integer n (1 ≤ n ≤ 10¹²).

Output. Print the value of f(n) modulo 2³².

Sample input	Sample output
7	10

SOLUTION

data structures – map, recursion

Algorithm analysis

Because of the limitation n ≤ 10¹², it is impossible to use a linear array to store the results of the values of the function f. For this purpose, we’ll use the map data structure.

It remains to write a recursive implementation of the function f, memoizing the intermediate results.

Algorithm realization

Declare the map m. Implement the computation of the function f. Since m[n] is of unsigned int type, all summations in the f function will be performed modulo 2³², as required in the problem statement.

map<unsigned long long, unsigned int> m;

unsigned int f(unsigned long long n)

{

If the value f(n) has not yet been calculated and, accordingly, the value m[n] has not yet been assigned, then its default value is m[n] = 0. If m[n] > 0, then f(n) has already been calculated and stored in m[n]. It makes no sense to compute it again, just return m[n].

if (m[n] > 0) return m[n];

The base case.

if (n <= 2) return m[n] = 1;

Compute f(n) depending on the parity of n.

if (n & 1)

return m[n] = f(6*n/7) + f(2*n/3);

else

return m[n] = f(n - 1) + f(n - 3);

}

The main part of the program. Read the value of n and print f(n).

scanf("%llu",&n);

printf("%u\n",f(n));

Java realization

import java.util.*;

public class Main

{

static Map<Long, Long> m = new HashMap<Long, Long>();

static long MOD = (long) Math.pow(2, 32);

public static long f(long n)

{

if (m.containsKey(n)) return m.get(n);

if (n <= 2)

{

m.put(n, (long)1);

return 1;

}

long res;

if (n % 2 == 1)

res = (f(6*n/7) + f(2*n/3)) % MOD;

else

res = (f(n-1) + f(n-3)) % MOD;

m.put(n,res);

return res;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

long n = con.nextLong();

System.out.println(f(n));

con.close();

}

}